Discrete Mathematics is one of the famous journals in discrete mathematics and combinatorics. The research areas covered by Discrete Mathematics include graph and hypergraph theory, enumeration, coding theory, block designs, the combinatorics of partially ordered sets, extremal set theory, matroid theory, algebraic combinatorics, discrete geometry, matrices, discrete probability, and parts of cryptography. Our paper has been accepted and will be published in volume 346, issue 4. The first student author Yuhao Liu is a senior undergraduate student. Professor Mingyu Xiao is the corresponding author.

Title: The (3, 3)-colorability of planar graphs without 4-cycles and 5-cycles

Authors: Yuhao Liu and Mingyu Xiao

In this paper, we study the colorability of a special kind of planar graph. A graph G is called (d1, . . . , dr)-colorable if its vertex set can be partitioned into r sets V1, . . . , Vr such that the maximum degree of the induced subgraph G[Vi ] of G is at most di for i ∈ {1, . . . , r}. The problem we study is a variant of famous Steinberg’s conjecture. Steinberg conjectured that every planar graph without 4-cycles and 5-cycles are (0,0,0)-colorable. Unfortunately, the conjecture does not hold. Based on it, there are a large number of research results. It is known that every planar graph without 4-cycles and 5-cycles is (3,4)-colorable or (2,6)-colorable. In this paper, we reduce the gap by proving that every planar graph without 4-cycles and 5-cycles is (3,3)-colorable.

Link to the paper: https://doi.org/10.1016/j.disc.2022.113306

实验室本科生在离散数学著名期刊Discrete Mathematics发表研究成果

近日，电子科技大学英才实验学院2019级数理基础科学专业本科生刘宇豪撰写的论文《The (3, 3)-colorability of planar graphs without 4-cycles and 5-cycles》被离散数学方向国际著名期刊《Discrete Mathematics》录用，并在2023年第4期刊出。该论文是在计算科学与工程学院算法与逻辑团队的肖鸣宇教授指导下完成的。

该论文研究的是平面图着色方面的问题。著名的平面图四色定理指的是任意一个平面图都可以用4种颜色对图中顶点进行染色使得任意相邻两个顶点被染不同颜色。一个后续研究问题是：只用3种或者2种颜色对一个平面图进行着色会有什么性质？很容易证明对一般平面图，没办法只用3种颜色进行着色。通过一系列深入研究后，Steinberg于1976年提出著名的猜想：不含长度为4和5的圈的平面图（用P(4,5)来表示这类平面图）可以用3种颜色来着色使得任意相邻两个顶点被染不同颜色。直到2017年，Steinberg的猜想才被证明是不成立的。我们不能保证每对相邻的顶点都染不同的颜色，但是可以使得染同一种颜色的点构成的图的度数尽量小。之前已知的结果是：P(4,5)类图可以用3种颜色进行着色使得每种相同颜色的点构成的图的度数不超过1；若只用2种颜色对P(4,5)类图进行着色，则可以使得每种相同颜色的点构成的图的度数不超过4。本文延续图着色方向里这条研究路线，进一步证明了，P(4,5)类图可以用2种颜色进行着色使得每种相同颜色的点构成的图的度数不超过3，改进了原有结果4。

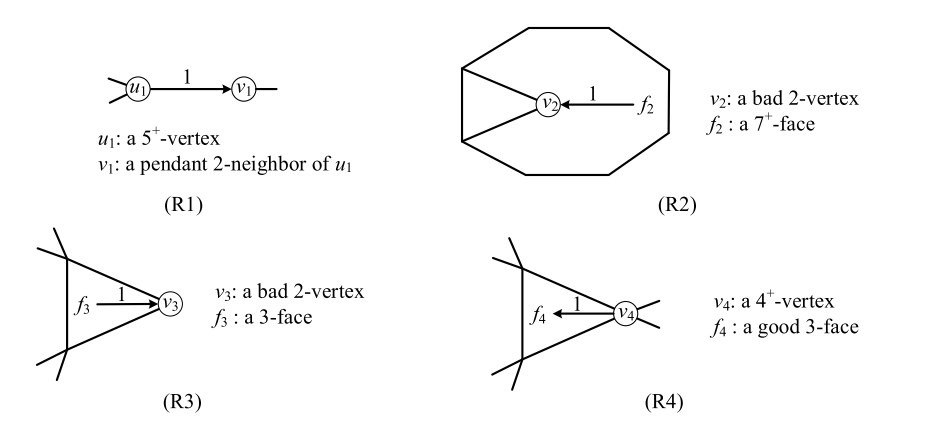
文中证明里用到的是权转移技术，我们先反设存在一个不能满足着色要求的图，然后对这个图上的顶点和面赋一种权值，使得图中所有顶点和面的权值总和是负的；然后通过一些规则在图中顶点和面之间进行权值的转移，在转移的过程中所有权值总和保持不变；但是转移全部完成后，我们可以计算出所有权值和为正的，得到这样一个矛盾，从而证明了这种不满足着色要求的图不存在。下图中给出了一些权转移的规则示例。

学生作者刘宇豪于2019年转入电子科技大学英才实验学院数理基础科学专业，大二开始进入计算机科学与工程学院算法与逻辑团队进行科研训练，先后参与多项图论、算法、组合优化方向的基础研究，已经在相关领域高水平期刊和会议上发表论文2篇，另1篇论文发表在算法领域顶级会议SODA 2023上。

电子科技大学算法与逻辑团队是由新西兰院士Bakh Khoussainov教授和算法著名专家肖鸣宇教授共同组建，面向全校师生开放的、致力于基础理论研究的团队。该团队关注算法、图论、逻辑、组合优化、机制设计等方面的基础难题，培养和激发学生及青年老师的理论研究兴趣。每年有10余名对算法和数学感兴趣的本科生进入团队学习，科研能力明显提升，高水平论文等学术成果层出不穷。长期以来，学生在多项科技竞赛中斩获奖项，多名学生在程序设计竞赛和数学建模竞赛中取得非常优异的成绩；在ACM程序设计竞赛中，团队多名学生打进了世界总决赛；在IEEE极限编程竞赛中团队学生连续两年获得世界第二名，五次进入世界前十名。

转自成电新闻 (阅读原文)